ぱうえる

Rustでデータ構造書いてみた（B木編）：前編

Rust競プロアドベントカレンダー2024

2024-12-11

はじめに

はじめまして．名古屋大学4年のぱうえるです．

昨年の記事「Rustでデータ構造書いてみた（スプレー木編）」に引き続き，今年も木の記事を書いていきたいと思います！

Rustは所有権によってポインタの扱いが厳格に定まっているため，木のように再帰的なデータ構造では実装に少しコツがいります．今回は，そんな困難を知ってなおRustでデータ構造を書きたいというRustaceanの一助となるべく，B木の実装を紹介していきたいと思います．

※間違いを見つけた場合にはTwitter: @penguineer までご連絡いただけるとありがたいです．

概要

前編

• B木の操作について説明したよ
  • 検索
  • 挿入

後編

• B木の操作について説明したよ
  • 削除
• RustでB木の実装をしたよ
  • ソースコード：https://github.com/kentakom1213/rust-btree
  • ここから動かせるよ：https://play.rust-lang.org/?version=nightly&mode=debug&edition=2021&gist=ad1ab8c52ba9988eb4654ba9110c04f3

B木とは

B木は，データを常にソートされた状態で管理することができるデータ構造の1種です．

また，赤黒木のように，データの挿入や削除で木のバランスが崩れることがないように自動的にバランスを保つ機能を持っています．（このような性質をもつ木構造を「平衡木」と呼びます．）

一方で，有名な平衡木の多くは分岐が2つまでしかない2分木ですが，B木は分岐数をいくらでも増やすことができるという特徴を持っています．

B木のメリット / 実用例

平衡2分木と比較した際，B木は分岐数が多いため，同じデータ数の場合では木の高さを低く抑えることができます．そのため，ノード間の移動のコストが大きい場合には2分木よりも高速に動作するようになります．

• ハードディスク上のデータ保管

  ハードディスクはその構造からシーケンシャルアクセスは高速，ランダムアクセスは低速という特性をもつため，ランダムアクセスの多い2分木は低速になってしまいます．一方，B木は1つのノードが持つデータ数が多いため，ランダムアクセスの回数を減らすことができ，高速に動作させられます．

• 多くのリレーショナルデータベース(RDB)の内部実装

  ハードディスクに置くことが多いからみたいです．

• Rustのソート済み集合

  Rustではキャッシュ効率の観点からソート済み集合にB木を採用しています．

  詳細：https://doc.rust-lang.org/std/collections/btree_map/struct.BTreeMap.html

B木の仕組み

では，実際にB木の中身がどうなっているのかを見ていきましょう！

B木の定義

B木には定義があり，この定義を満たすように挿入や削除を行うことで木の平衡を保つことができます．（よくわからない場合は飛ばして読み進めても大丈夫です）

B木 $T$ は，以下の性質をもつ根付き木です．（定義はアルゴリズムイントロダクション[1]に準拠しましたが，多少端折っている部分もあるので詳細はそちらを参照してください）

1. 各ノード $x$ は以下の属性を持つ
   1. $x$ に格納されているキーの数 $x.n$ （単に $x$ のサイズともいう）
   2. 格納されている $x.n$ 個のキー $x.\mathit{key}_1, x.\mathit{key}_2, \ldots, x.\mathit{key}_n$ は昇順に並べられている
   3. $x$ が葉であればTrue，内部ノードであればFalseとなるブール値 $x.\mathit{leaf}$
2. ノード $x$ が内部ノードであれば，$x.n+1$ 個のポインタ $x.c_1, x.c_2, \ldots, x.c_{n+1}$ を持つ
3. 各ノードについて，キー $x.\mathit{key}_i$ と $x.\mathit{key}_{i+1}$ の間にある子 $x.c_i$ が持つ値 $k_i$ は
   $$x.\mathit{key}_i \le k_i \le x.\mathit{key}_{i+1}$$

   となる．（両端の子についても同様）

4. すべての葉は同じ深さを持つ
5. 1つのノードが格納できるキーの数には上限と下限が存在する．これはB木の最小次数と呼ばれる値 $t~(t\ge 2)$ を用いて表される．（最小次数はB木 $T$ に固有の定数である）
   1. 根を除くすべてのノードは少なくとも $t-1$ 個のキーをもつ．したがって，根を除くすべての内部ノードは少なくとも $t$ 個の子をもつ．木が空でなければ根は少なくとも $1$ 個のキーをもつ．
   2. どのノードも最大 $2t-1$ 個のキーを持つことができる．したがって，内部ノードは最大 $2t$ 個の子を持つことができる．ちょうど $2t-1$ 個キーをもつ内部接点は飽和しているという．

例

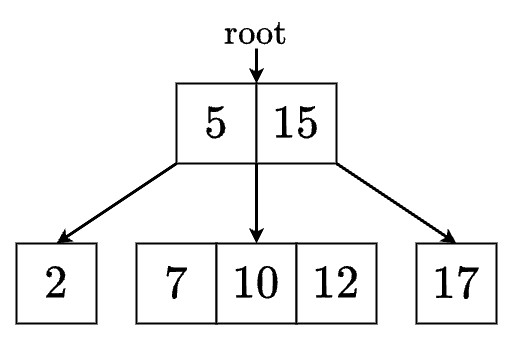
最小次数が $t=2$ のとき，各ノードのキーは $t-1=1$ 個以上 $2t-1 = 3$ 個以下であり，下の図のようになります．

最小次数が $t=3$ のとき，根以外の各ノードのキーは $t-1 = 2$ 個以上 $2t-1 = 5$ 個以下であり，下図のようになります．

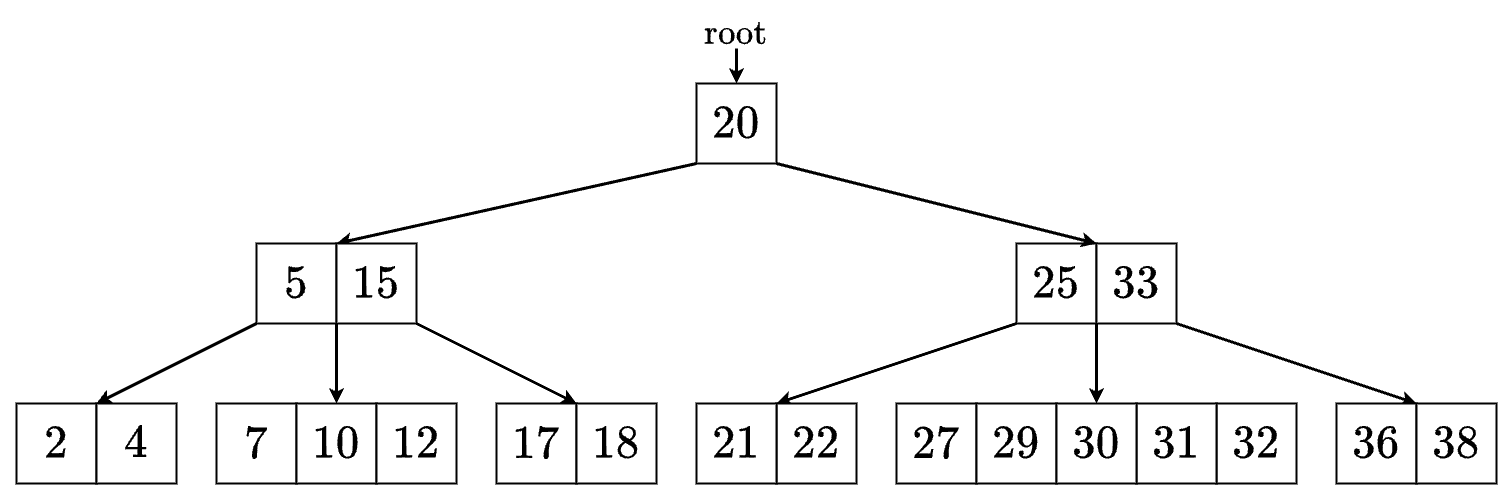
以下，上の $t=3$ の木を用いて解説してきます．

検索

B木 $T$ に値 $k$ を持つキーが存在するか調べる場合を考えます．以下のようなアルゴリズムで実現できます．

アルゴリズム: $\text{B-Tree-Find}(T, k)$

1. $x$ を$T$ の根へのポインタで初期化する．
2. $x$ が葉でない間以下を繰り返す．
   1. $x$ の各キーについて順に，
      1. $k$ がキーより小さければ $x$ をキーの左の子に更新して2に戻る．
      2. $k$ がキーに一致すればTrueを返す．
   2. $k$ が $x$ のどのキーよりも大きければ $x$ を $x$ の最も右の子に更新する．
3. $x$ が葉である場合，$x$ に $k$ と等しいキーがあればTrue，そうでなければFalseを返す．

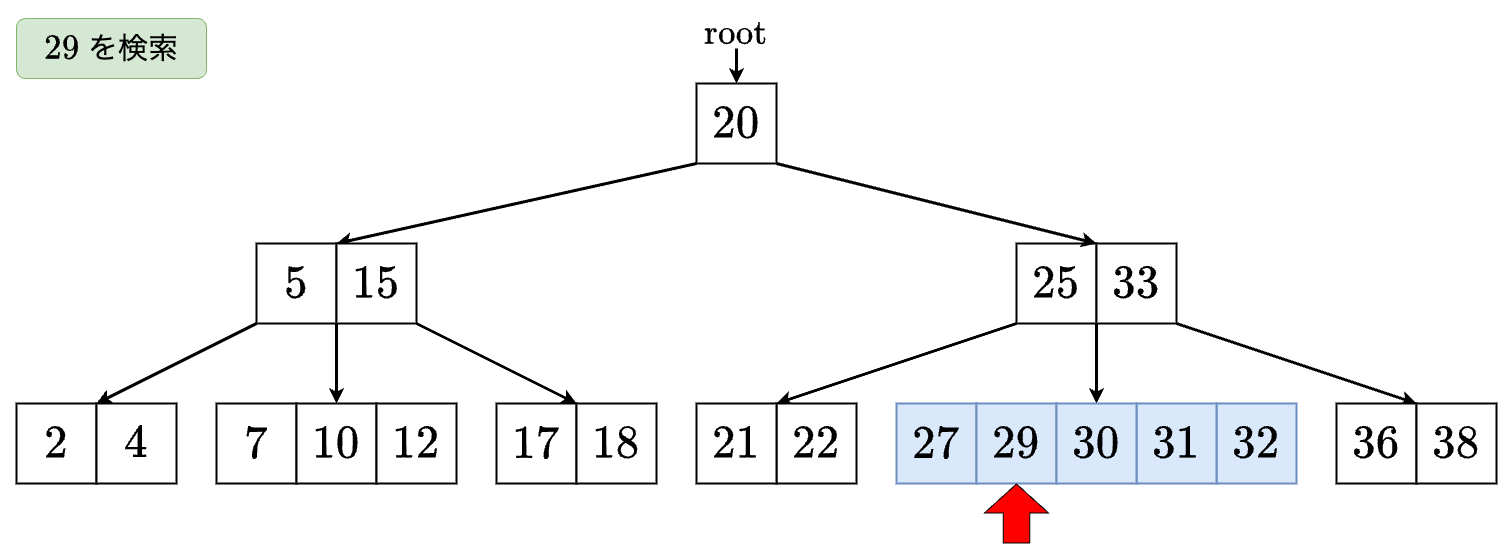
例

値 $29$ を検索する場合は以下のようになります．

1. $20 < 29$ なので右の子に移動します．

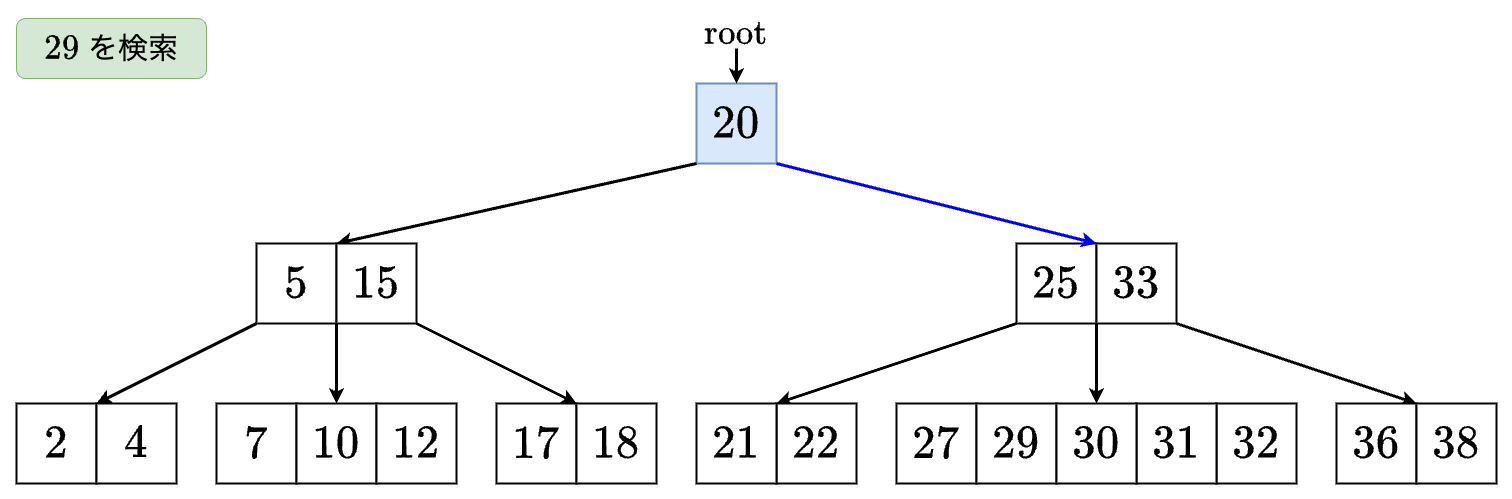
1. $25 < 29 < 33$ なので $33$ の左の子に移動します．

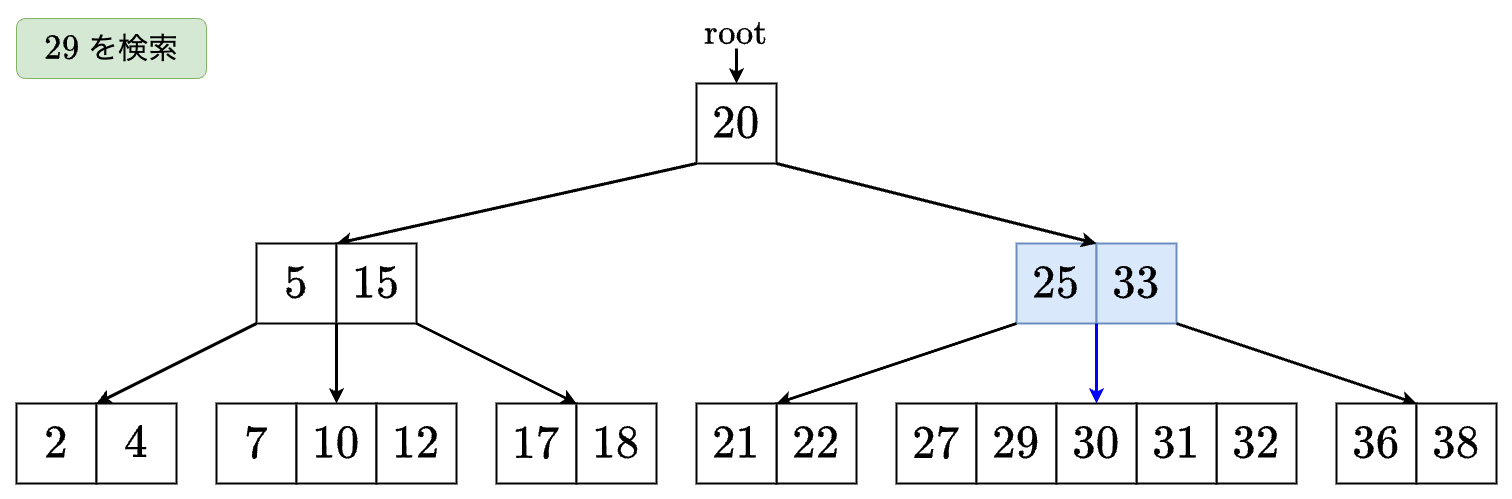
1. $29$ のノードが見つかったのでTrueを返します．

挿入

次に挿入について考えます．B木への挿入は，検索と同様に適切なノードをたどりながら行いますが，飽和したノードに挿入されないよう，ノードの分割を行いつつたどっていきます．

B木 $T$ にキー $k$ を挿入するアルゴリズムは以下のとおりです．

アルゴリズム: $\text{B-Tree-Insert}(T, k)$

1. $x$ を$T$ の根へのポインタで初期化する．
2. $x$ が葉でない間以下を繰り返す．
   1. $x$ が飽和していれば，ノードの分割を行う．
   2. $x$ の各キーについて順に，
      1. $k$ がキーより小さければ $x$ をキーの左の子に更新して2に戻る．
   3. $k$ が $x$ のどのキーよりも大きければ $x$ を $x$ の最も右の子に更新する．
3. 葉への挿入でキー $k$ を挿入する．

ノードの分割，葉への挿入については以下のとおりです．

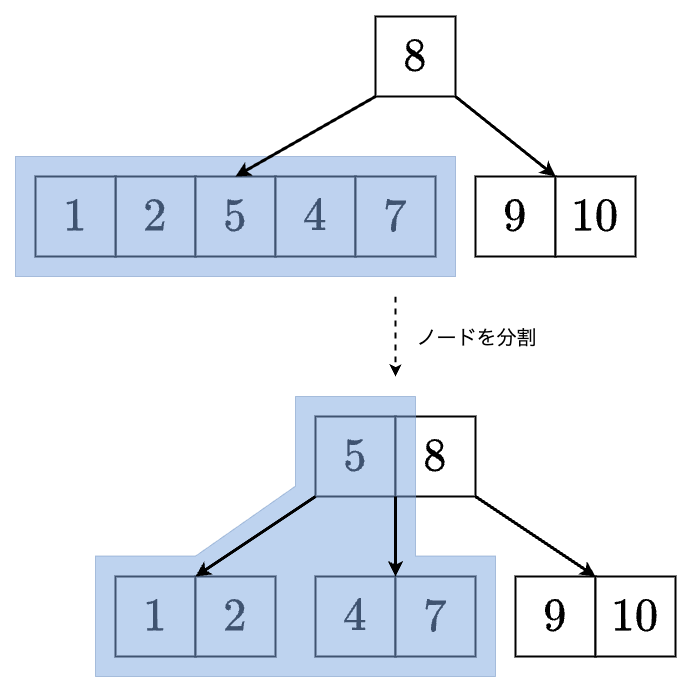
ノードの分割

$2t-1$ 個のキーをもつノードを

• 小さい方から $t-1$ 個
• 中央値 $1$ 個
• 大きい方から $t-1$ 個

に分割します．小さい方から $t-1$ 個，大きい方から $t-1$ 個をそれぞれ別のノードに移し，中央値を親に移動します．

葉への挿入（サイズが 2t-2 以下のとき）

ノードが葉であり， $2t-2$ 個以下のキーしか持っていない場合はソート済み配列への挿入と同じようにすればよいです．

葉への挿入（サイズが 2t-1 個のとき）

ノードが葉であり，ちょうど $2t-1$ 個のキーを持っている場合には，直接挿入することができません．（キーの数が $2t$ 個になってB木の条件を満たさなくなってしまうため）

そこで，ノードを分割してから挿入します．

例

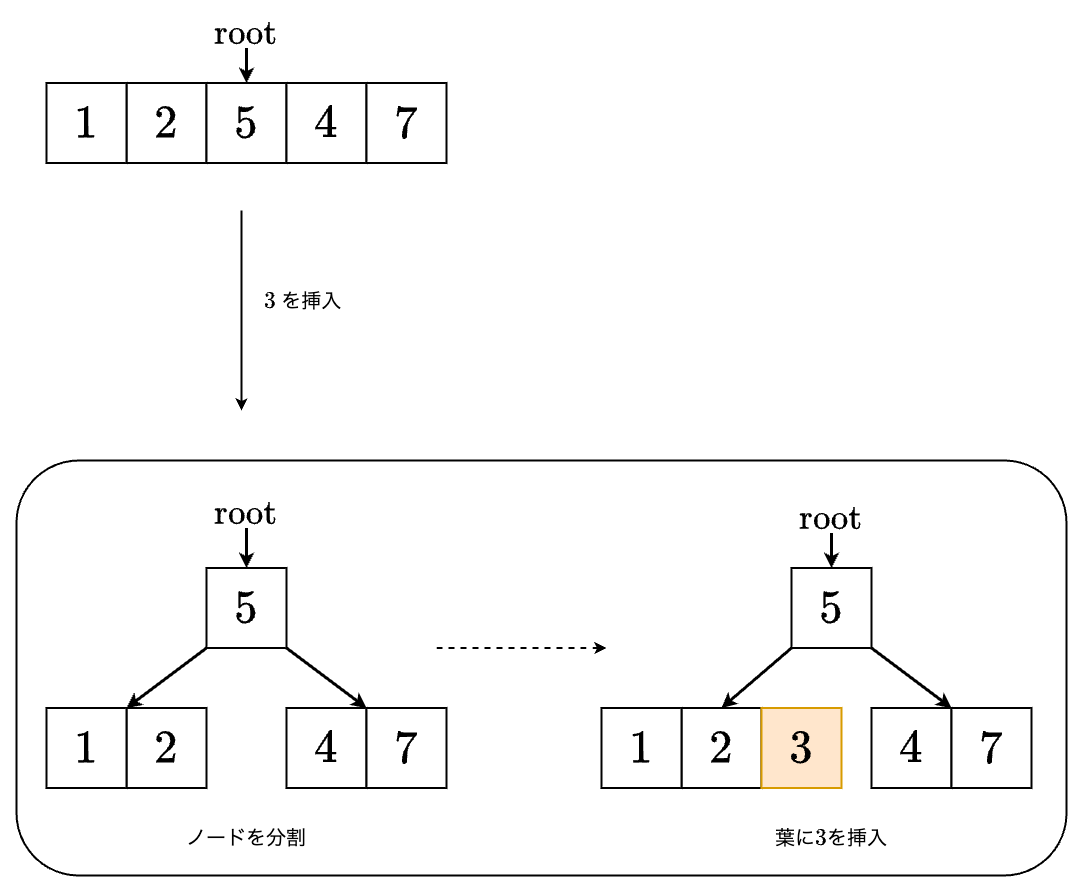
値 $28$ を挿入する場合は以下のようになります．

1. 右の子に進みます．

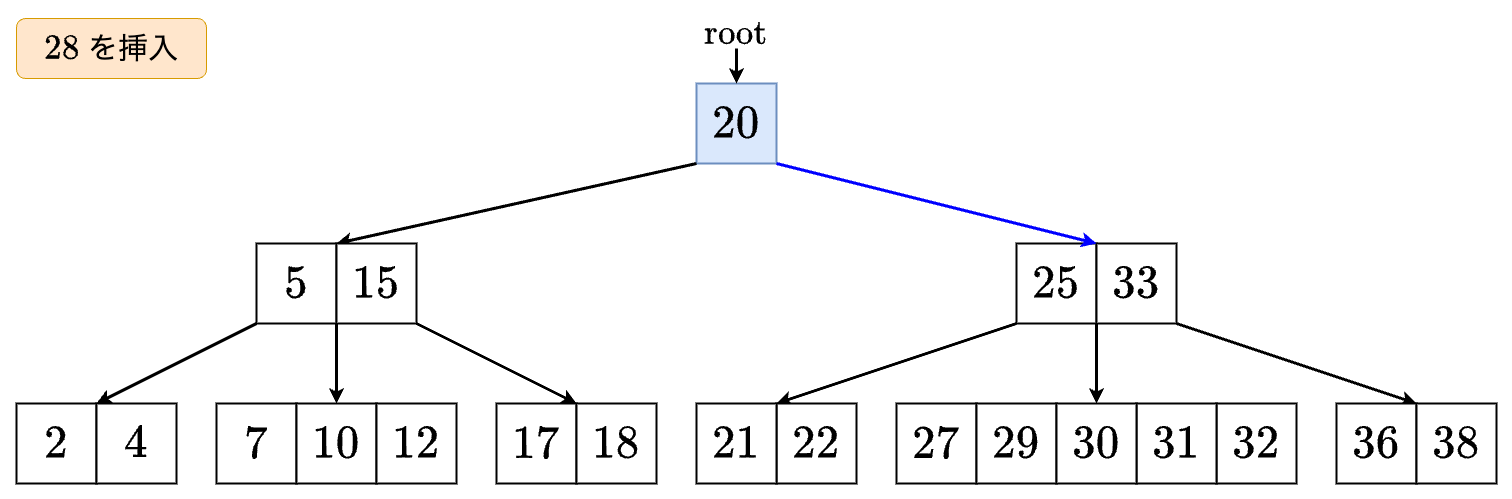
1. $33$ の左の子に進みます．

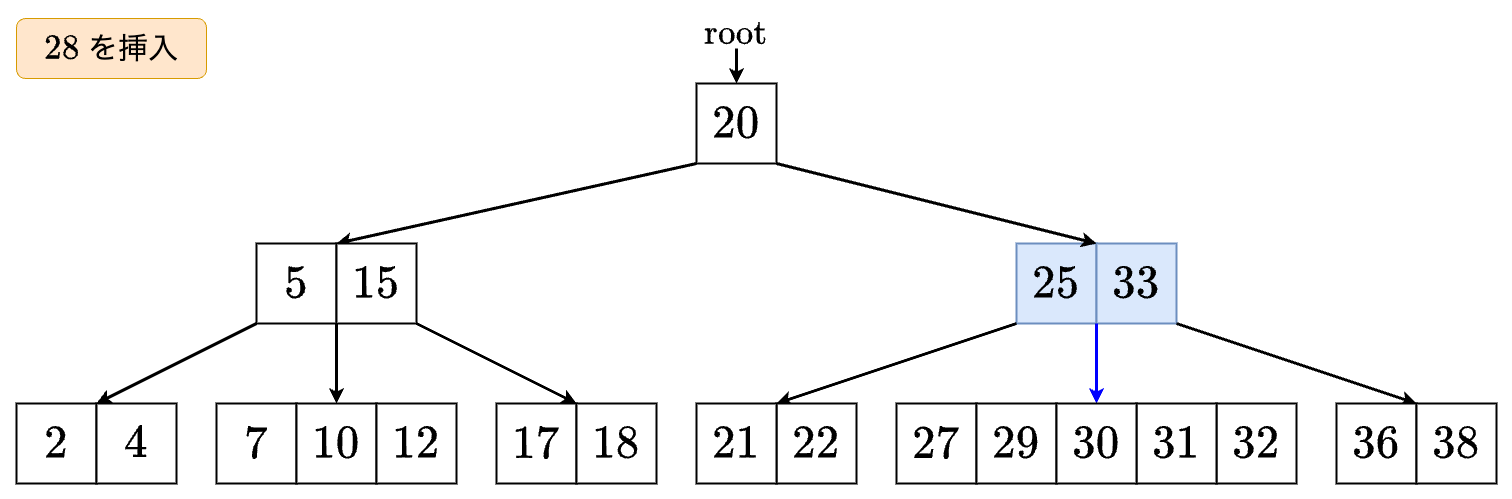
1. すでに5個のキーを持っているので，ノードを分割します．

   その後，$30$ の左の子に進みます．

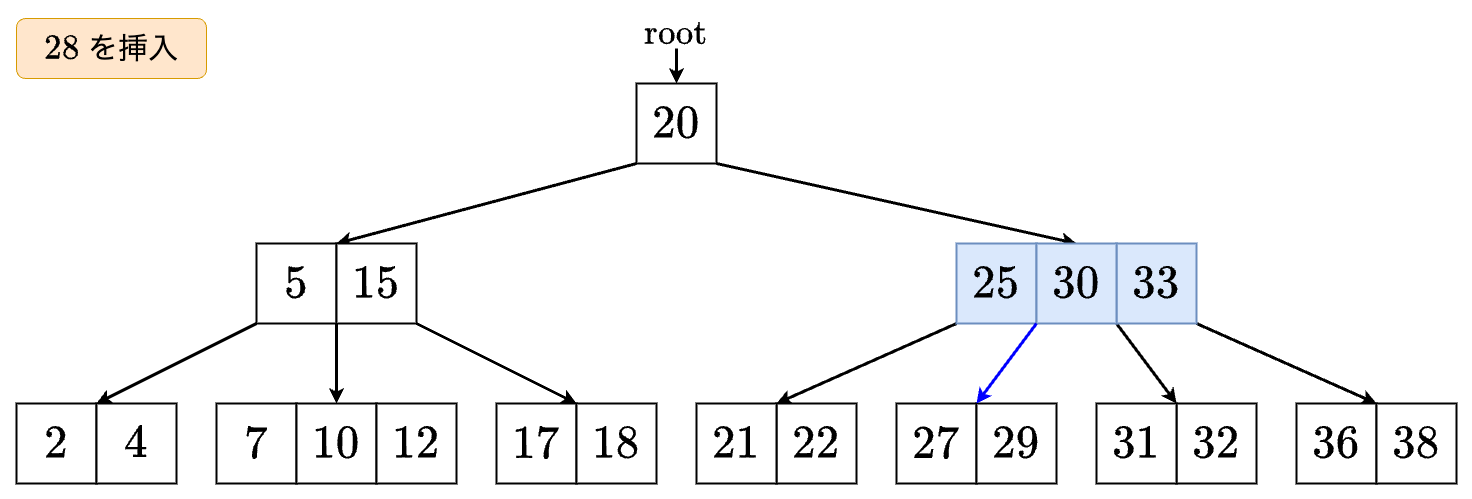
1. $27,29$ の間に挿入します．

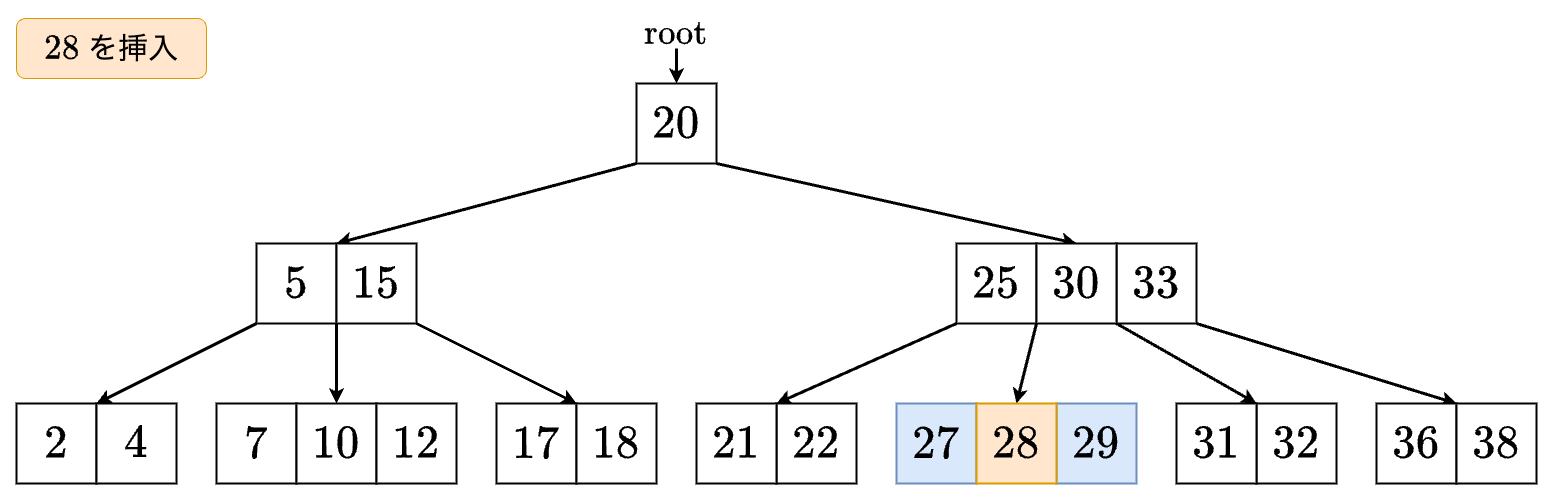
→ これで挿入ができました！

前編のまとめ

ここまで，

• B木のメリット
• B木の定義
• B木の操作
  • 値の検索
  • 値の挿入

を見てきました．

前編の内容はここまでです．後編もぜひご覧ください！