Rustでデータ構造書いてみた（B木編）：後編

はじめに

この記事は「Rustでデータ構造書いてみた（B木編）：前編」の続きです．まだ読んでいないかたは先にそちらをご参照下さい．

概要

前編

• B木の操作について説明したよ
  • 検索
  • 挿入

後編

• B木の操作について説明したよ
  • 削除
• RustでB木の実装をしたよ
  • ソースコード：https://github.com/kentakom1213/rust-btree
  • ここから動かせるよ：https://play.rust-lang.org/?version=nightly&mode=debug&edition=2021&gist=ad1ab8c52ba9988eb4654ba9110c04f3

B木の仕組み

削除

B木からの削除は場合分けが多くかなり複雑ですが，1つづつみていきましょう．

B木 $T$ からキー $k$ を削除するアルゴリズムは以下のとおりです．（ノード $k$ が $T$ に存在することを仮定します）

アルゴリズム: $\text{B-Tree-Remove}(T, k)$

1. $x$ を$T$ の根へのポインタで初期化する

その後，以下の場合分けにしたがう．

1. キー $k$ がノード $x$ に存在し，$x$ が葉であるとき，$k$ を $x$ から削除する
2. キー $k$ がノード $x$ に存在し，$x$ が内部ノードであるとき，
   1. $x$ における $k$ の直前の子 $y$ のサイズが $t$ 以上のとき

      → $y$ の部分木の最大値 $k'$ を削除し，$x$ において $k$ を $k'$ に置き換える

   2. $x$ における $k$ の直後の子 $z$ のサイズが $t$ 以上のとき

      → $z$ の部分木の最小値 $k'$ を削除し，$x$ において $k$ を $k'$ に置き換える

   3. $y$，$z$ のサイズがいずれも $t-1$ のとき

      → $y,k,z$ をこの順で併合し，併合したノードから $k$ を削除する

3. キー $k$ がノード $x$ に存在しないとき，キー $k$ を部分木に含むような $x$ の子 $x.c_i$ を特定する．$x.c_i$ のサイズが $t-1$ のとき，ステップ3-1, 3-2のいずれかを実行し，$x$ の適切な子に再帰する．
   1. $x.c_i$ のサイズが $t-1$ であり，かつ，$x.c_{i-1}$ または $x.c_{i+1}$ のサイズが $t$ のとき

      → $x$ のキーを $x.c_i$ に移す．その代わりとして，$x.c_{i-1}$ の最大値，または $x.c_{i+1}$ の最小値を削除し，元あった場所に挿入する．$x.c_{i-1}$ または $x.c_{i+1}$ の適切な子ポインタも $x.c_i$ に移動する．

   2. $x.c_i$ のサイズが $t-1$ であり，かつ，$x.c_{i-1}$ と $x.c_{i+1}$ のサイズがどちらも $t-1$ のとき

      → $x.c_i$ をどちらかの兄弟と併合する

ノードの併合については以下で説明します．

ノードの併合

ノード $x$ のキー $x.\mathit{key}_i$ の左の子 $x.c_i$ ，右の子 $x.c_{i+1}$ のサイズがともに $t-1$ であるとき， $k$ ，$x.c_{i+1}$ のキーをこの順に $x.c_i$ に移し，$x.c_{i+1}$ を削除します．$z.c_{i+1}$ 子のポインタについても適切に移動します．

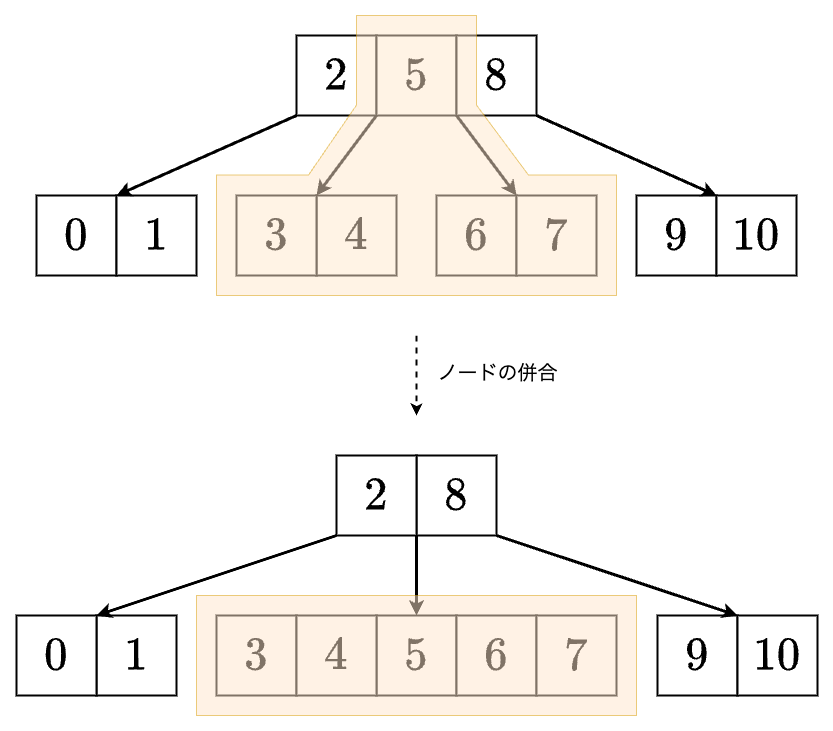
例で見ていきましょう．

1. 葉からの削除

値 $27$ を削除する場合を考えます．

1. $20$ の右の子に進みます

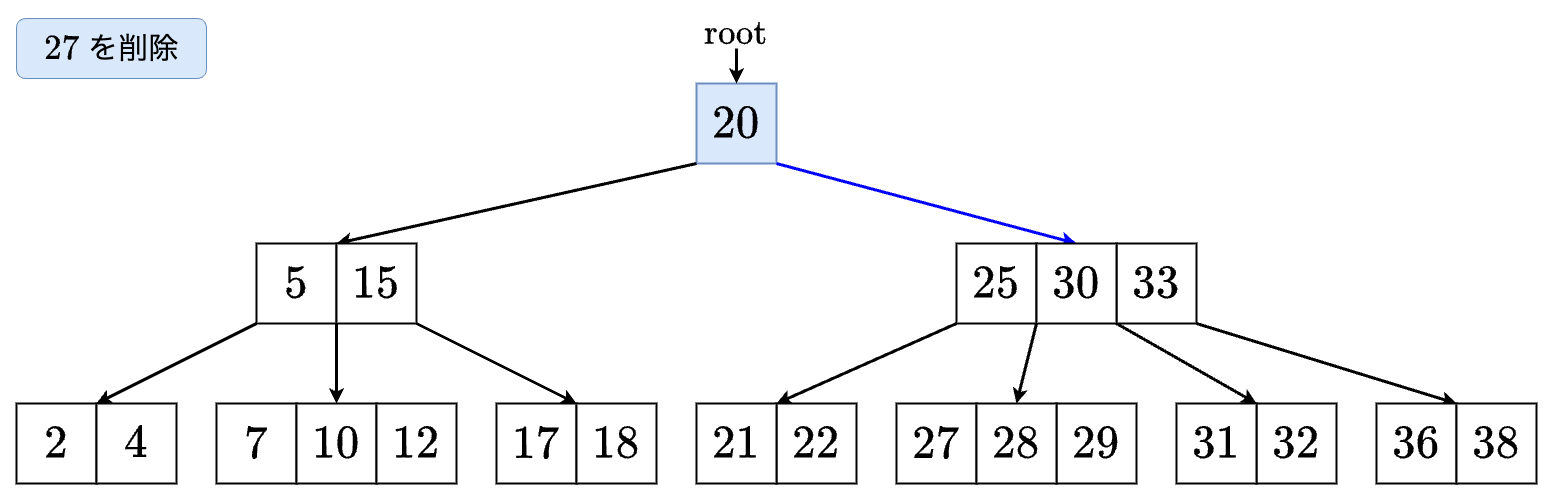
1. $30$ の左の子に進みます．

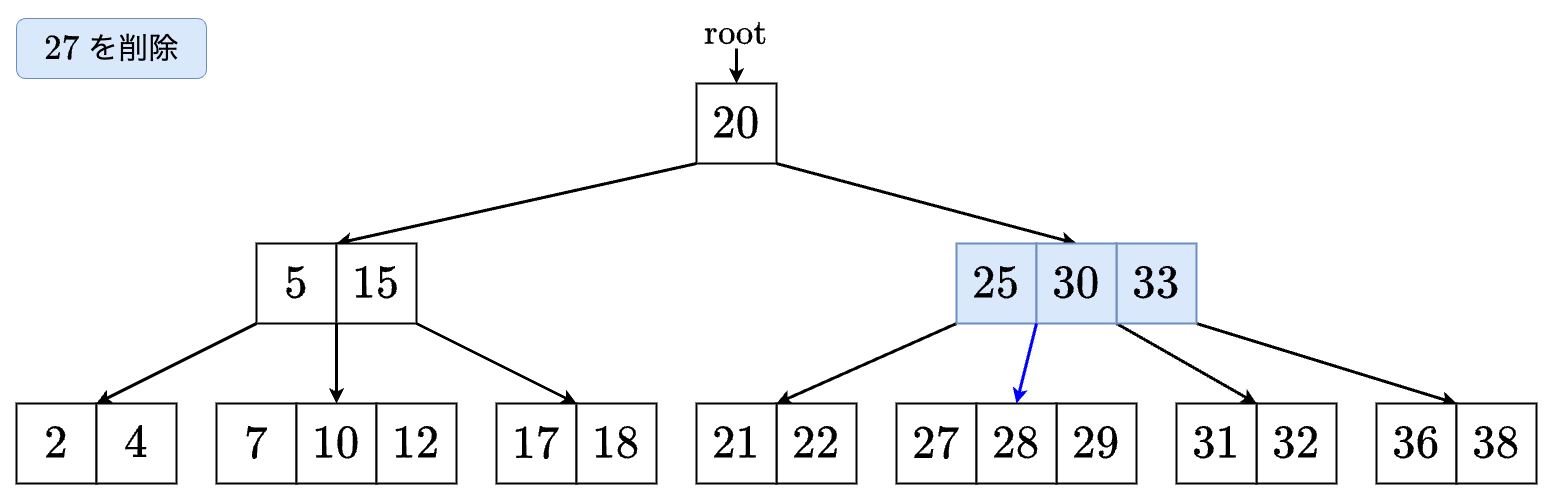
1. $27$ を発見したので削除します．

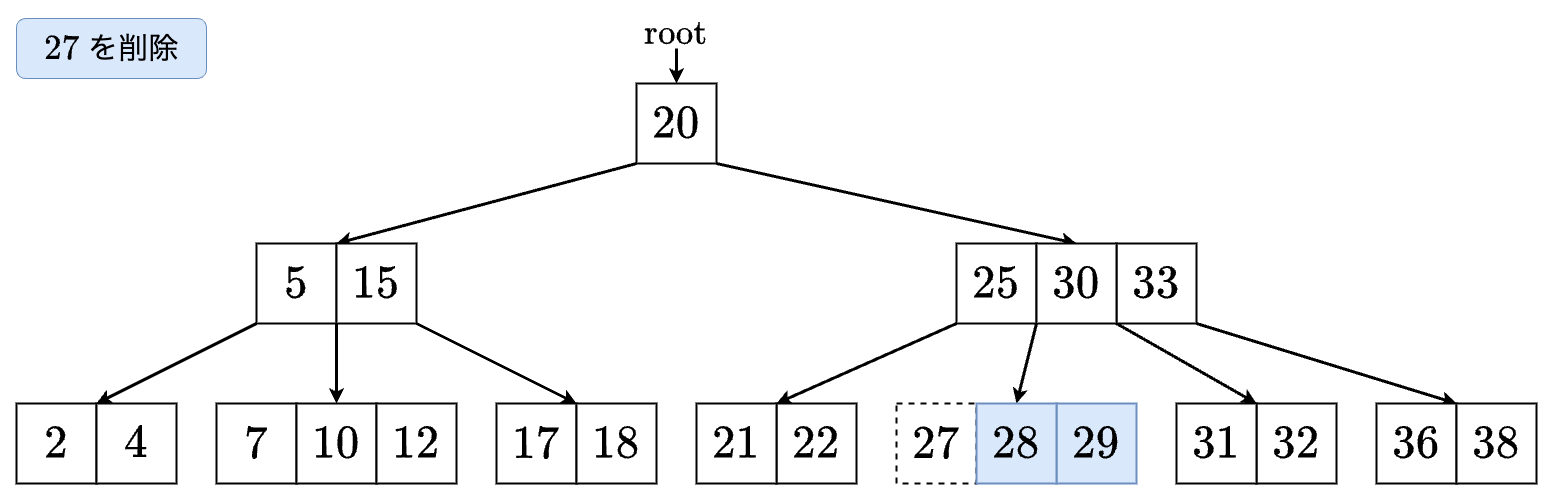
1. これで完了です．

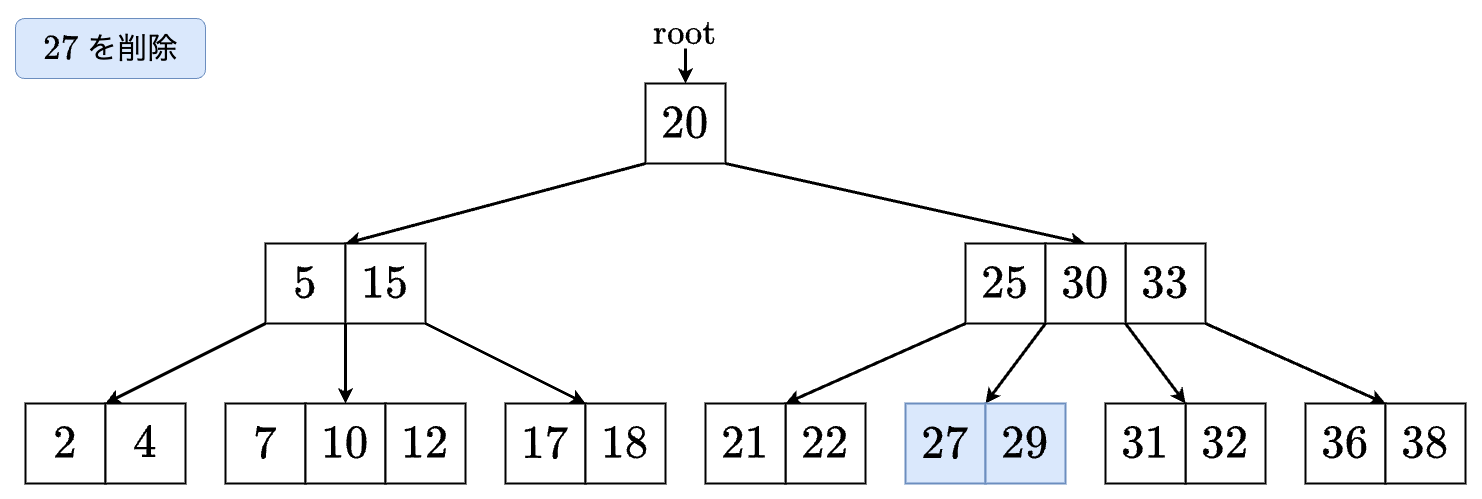
2-1. 内部ノードからの削除（左右のいずれかの子のサイズが t 以上）

値 $15$ を削除する場合を考えます．

1. $20$ の左の子に進みます．

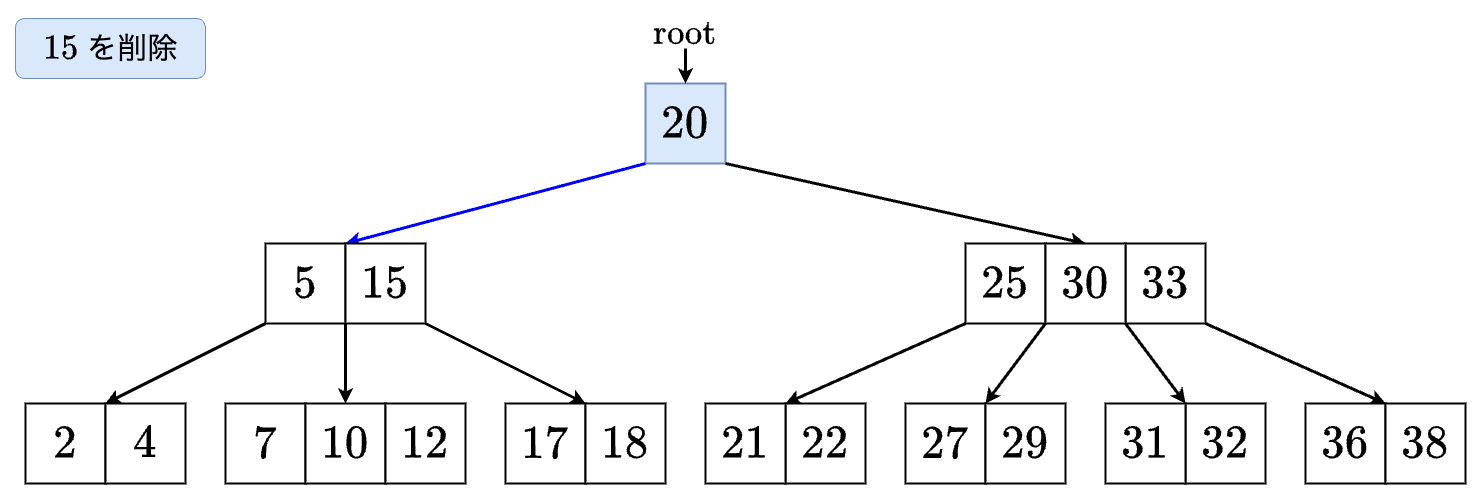
1. $15$ を発見しますが，そのまま消すことはできません． $15$ の左の子のサイズが $t ~(=3)$ 以上なので $15$ の左の子から最大値 $12$ を削除します．

1. $15$ を削除し，その位置を先ほど取ってきた $12$ を入れて完了です．

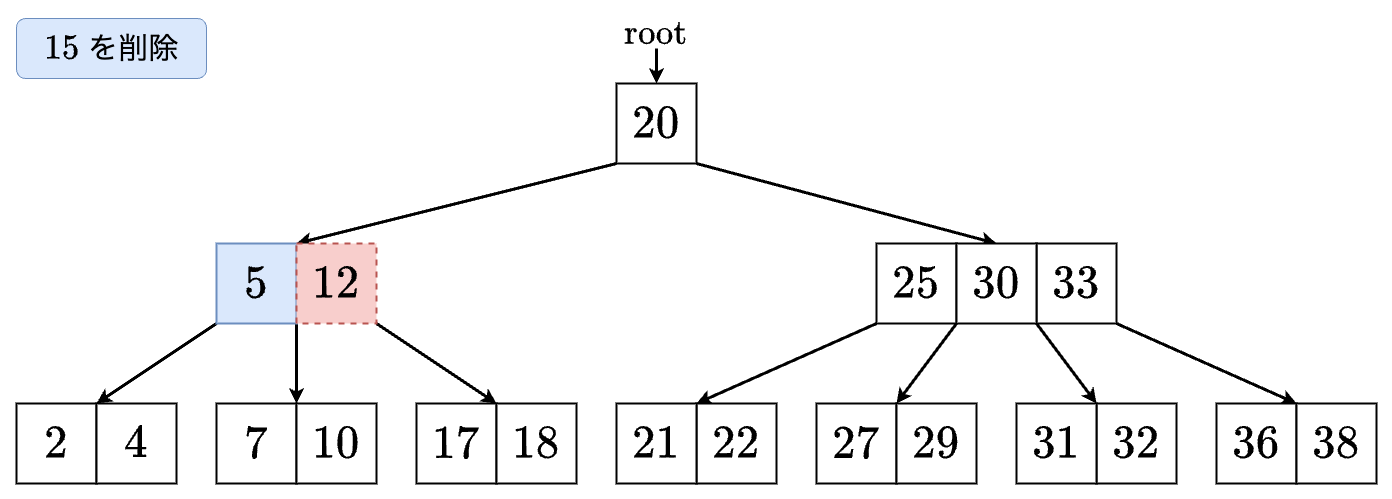
2-2. 内部ノードからの削除（左右の両方の子のサイズが t-1 以下）

値 $30$ を削除する場合を考えます．

1. $20$ の右の子に進みます．

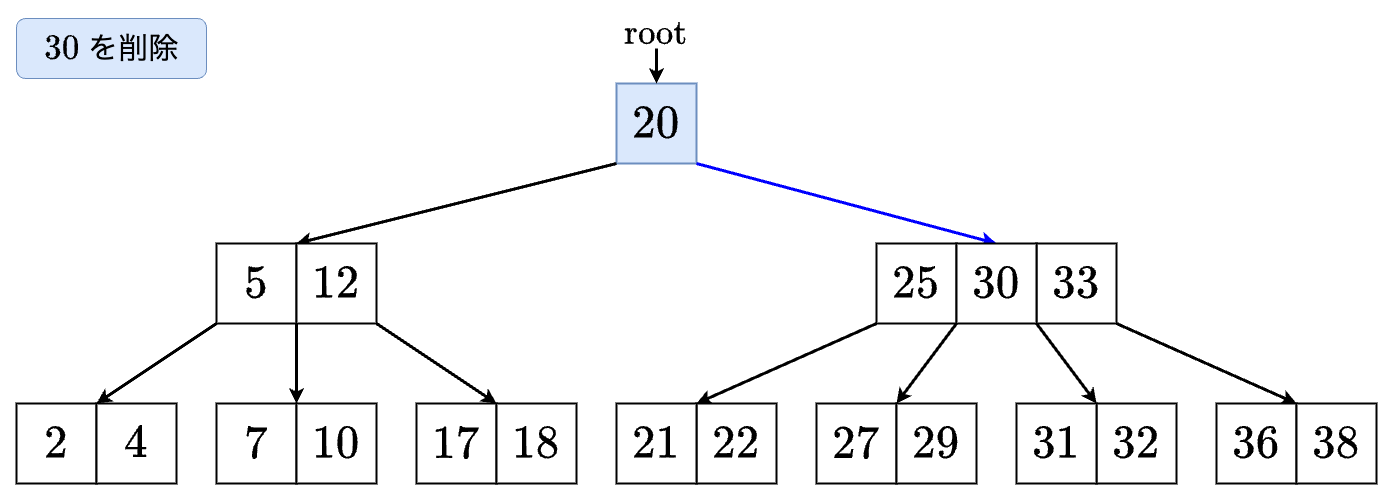
1. $30$ を発見しますが，そのまま消すことはできません． $30$ の左の子と右の子のサイズがともに $t-1~(=2)$ なので，それらをマージします．

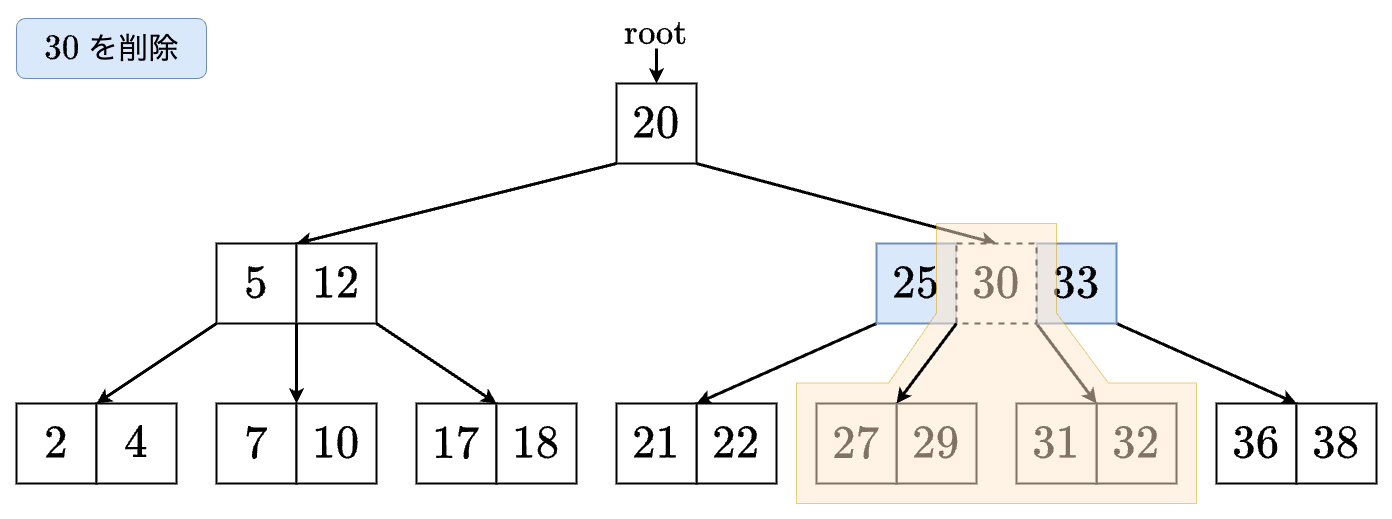
1. マージされた頂点に進みます．

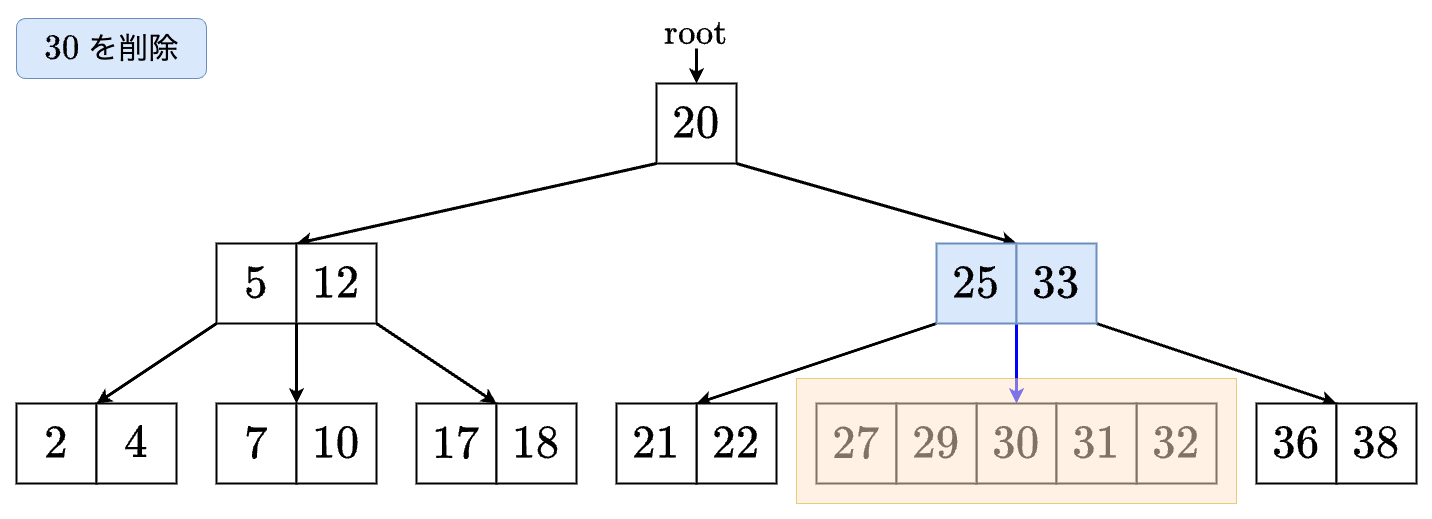
1. マージされた頂点から値を削除します．

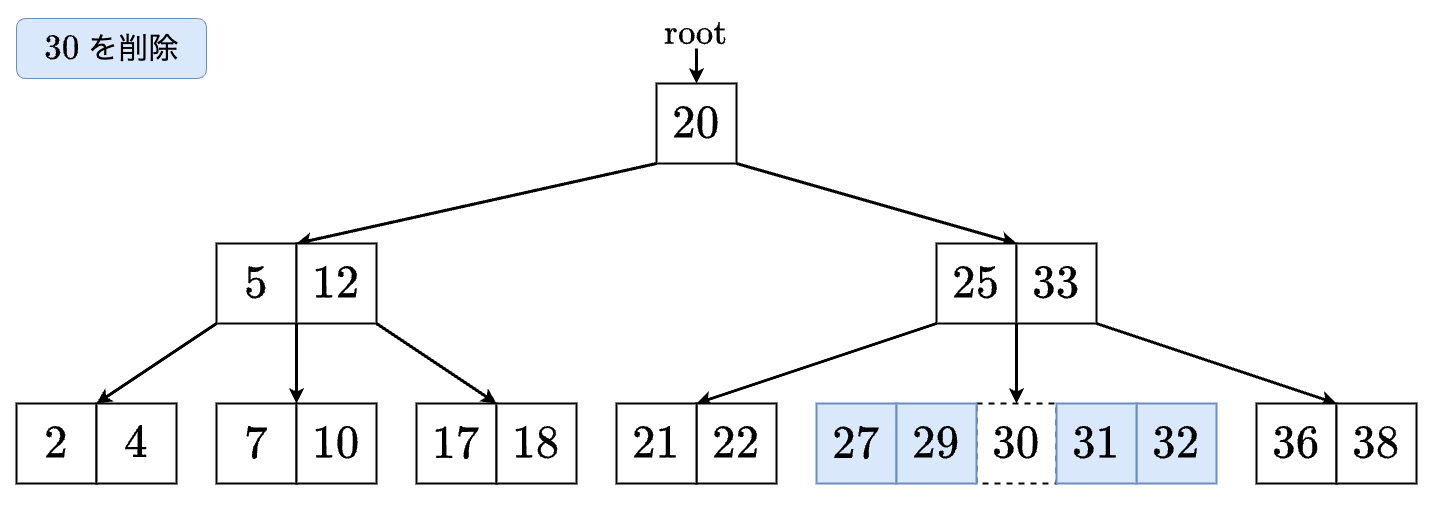
1. これで完了です．

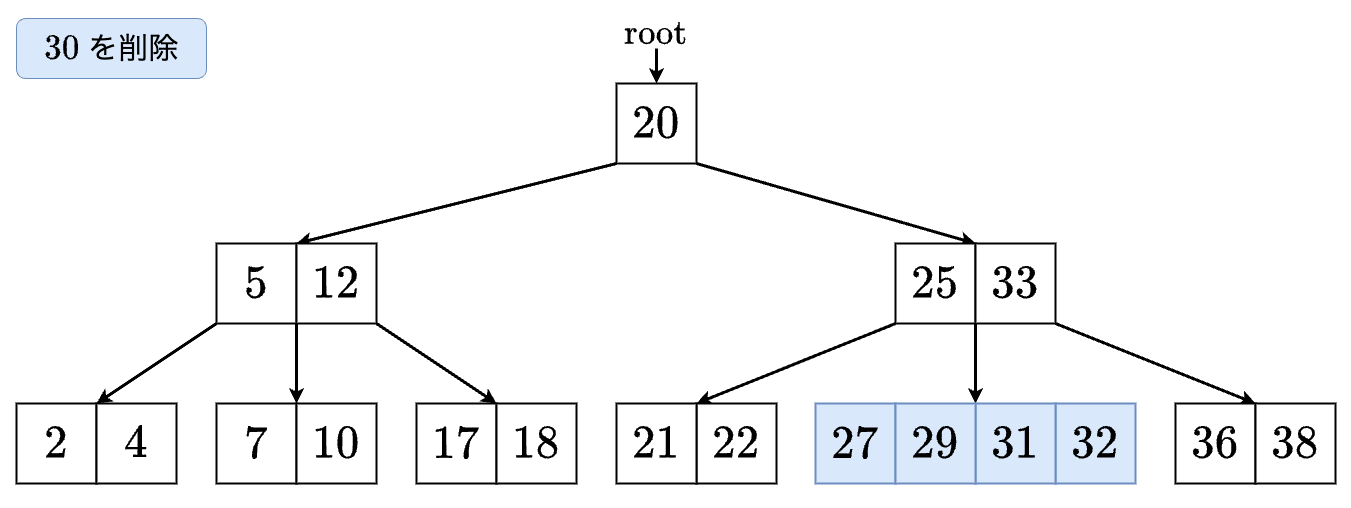
3-1,2. サイズが t-1 以下のノードに進む場合

値 $22$ を削除する場合を考えます．

1. 根ノードの2つの子のサイズがともに $t-1~(=2)$ なので，これらをマージします．（3-2）

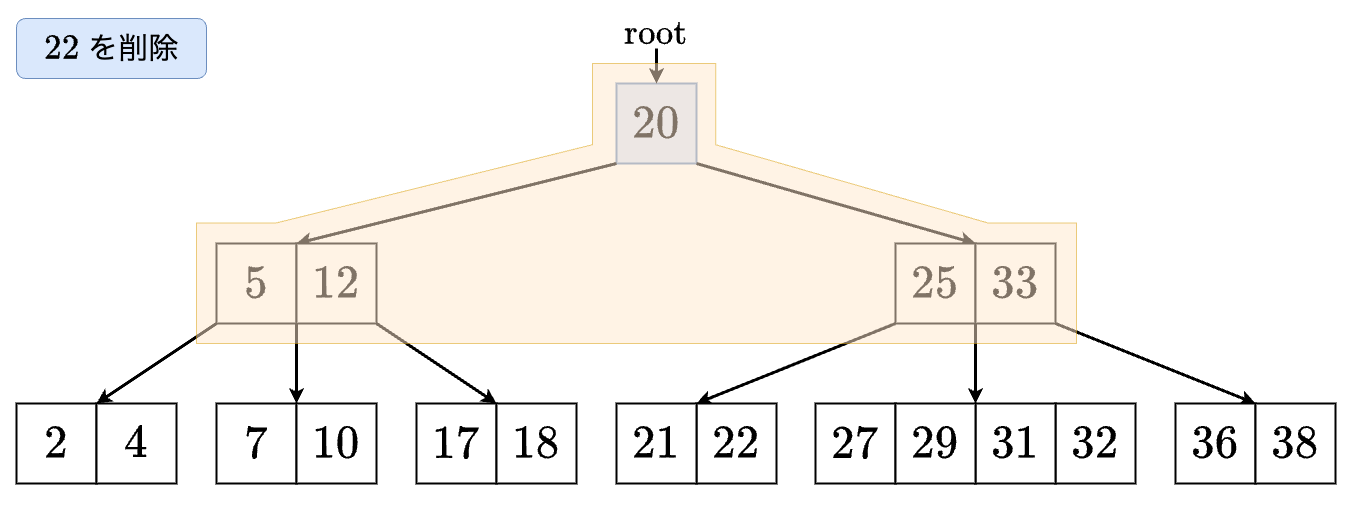
1. マージが完了しました．

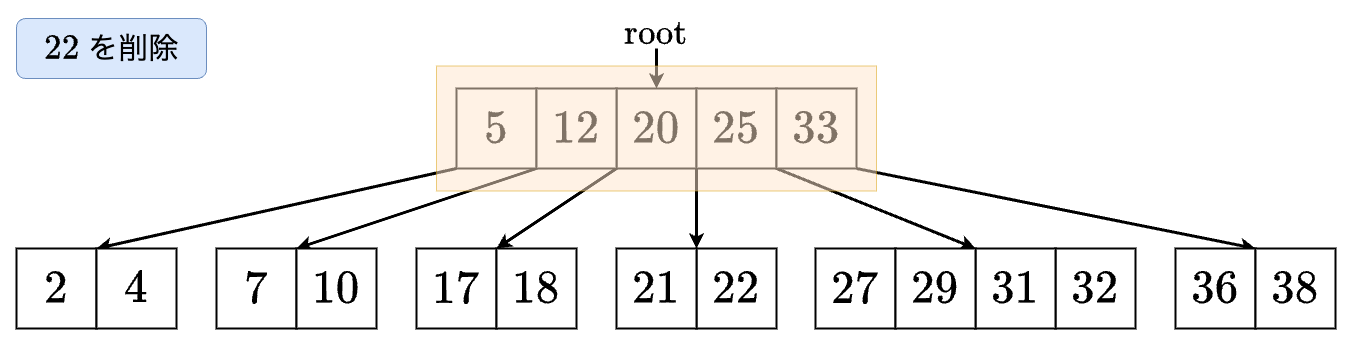
1. $25$ の左の子に進みますが，このノードのサイズは $t-1$ しかないのでそのままでは進めません．

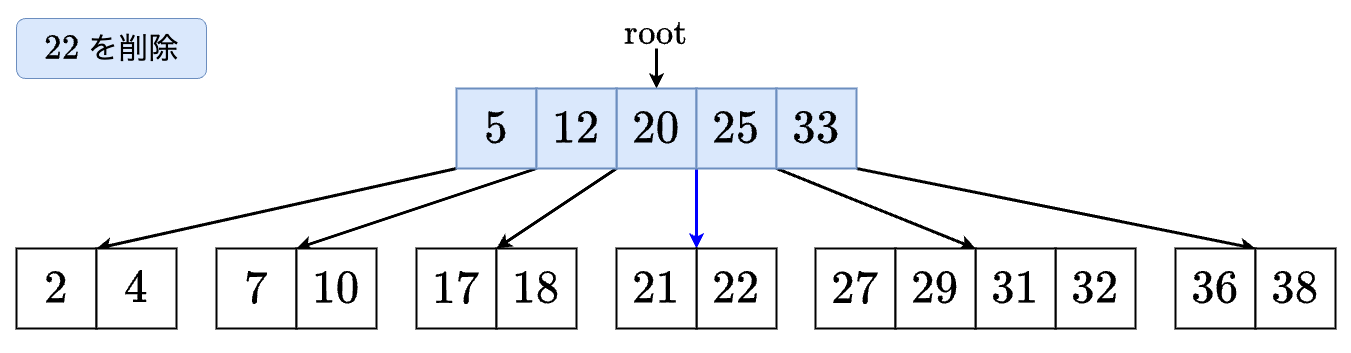
1. $25$ の右の子のサイズは $t~(=3)$ 以上なので，ここから最小値を削除します．

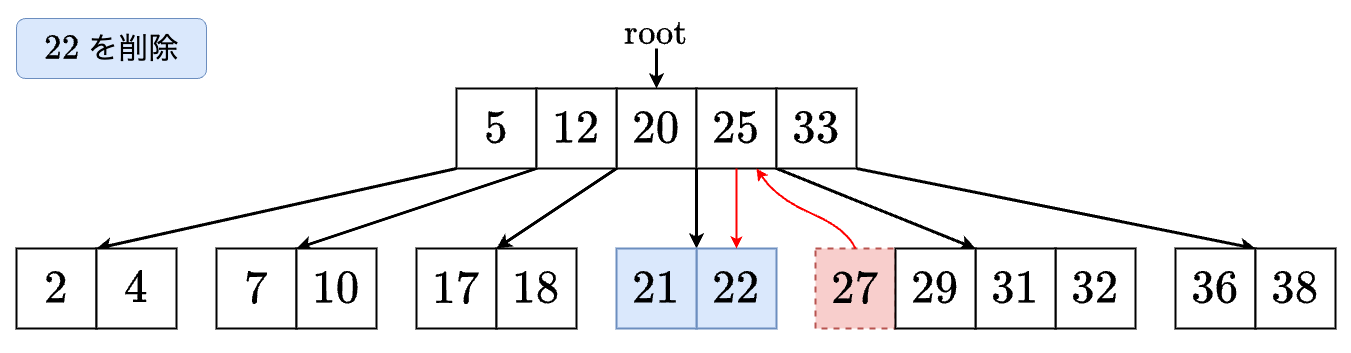
1. 削除した最小値を左の子に移します．これで左の子のサイズが $t$ 以上になりました！ $27$ の左の子に移動します．

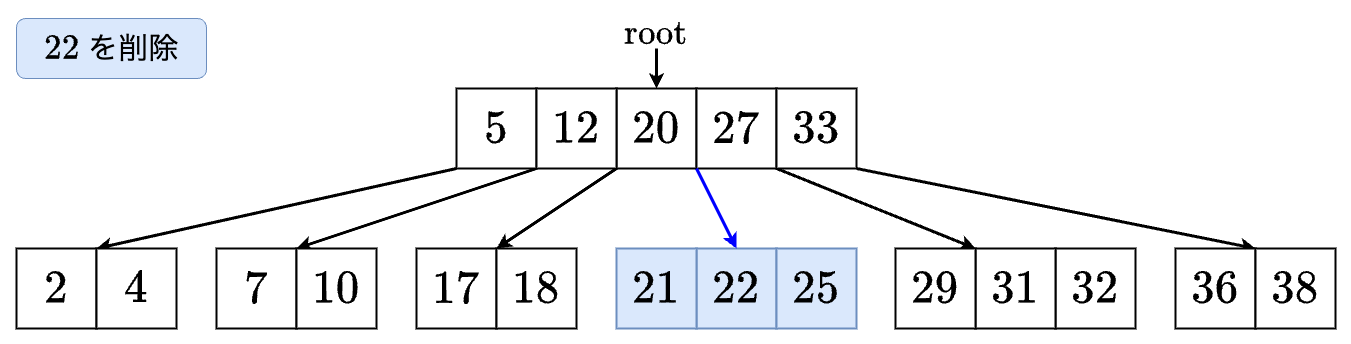
1. $22$ を削除します．

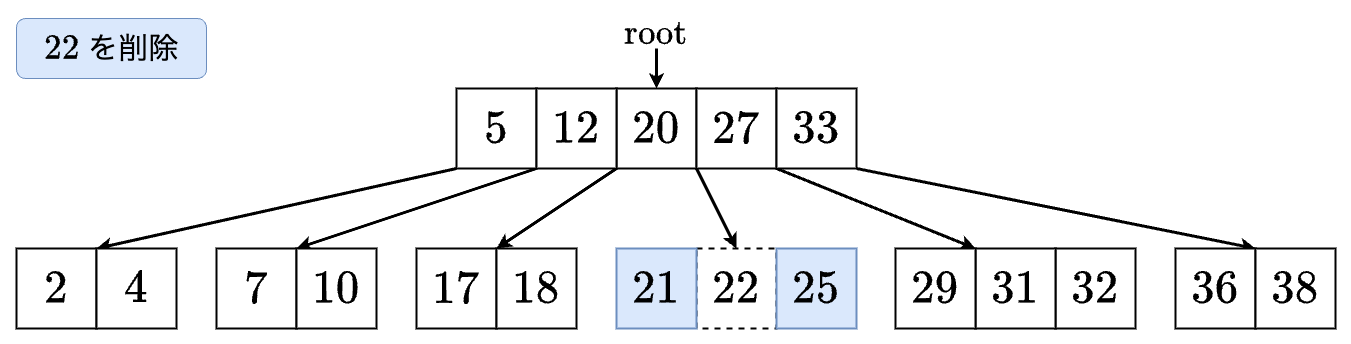
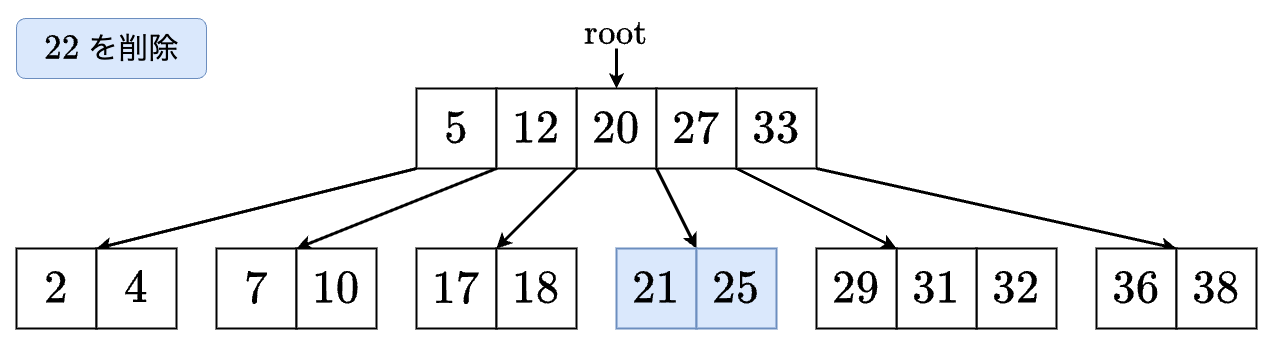
1. これで完了です！

実装

実装はこちらにアップロードしました：https://github.com/kentakom1213/rust-btree

各操作については，

• 検索：https://github.com/kentakom1213/rust-btree/blob/main/src/node/search.rs
• 挿入：https://github.com/kentakom1213/rust-btree/blob/main/src/node/insert.rs
• 削除：https://github.com/kentakom1213/rust-btree/blob/main/src/node/remove.rs

をご覧ください．

また，動かして遊べるページも作ったのでぜひ試してみてください．

https://play.rust-lang.org/?version=nightly&mode=debug&edition=2021&gist=ad1ab8c52ba9988eb4654ba9110c04f3

後編のまとめ

ここまで，

• B木の操作
  • 値の削除
• B木の実装

を見てきました．この記事の内容は以上となります．

おわりに

ここまで読んでくださりありがとうございました．

今年のクリスマスツリーはB木できまりですね！

メリークリスマス🎅

参考文献

1. 浅野哲夫．「アルゴリズムイントロダクション」第3版 第2巻，近代科学社，2012年，p106-121
2. B木，Wikipedia，https://ja.wikipedia.org/wiki/B木，2024年12月3日閲覧